Orbital: A New Frontier in Stablecoin Liquidity
Introduction
In DeFi’s short but explosive history, a few architectural innovations have fundamentally reshaped how we allocate capital. Uniswap made market making permissionless. Curve optimized it for stablecoins, assuming 1:1 pegs. Morpho gave lenders the power to choose which risks they take, turning AAVE’s monolithic lending model into a personalized risk frontier.
Orbital brings that same spirit of design evolution to the AMM space.
Instead of assuming stablecoin pegs are always reliable, Orbital embraces the opposite: pegs break and when they do, liquidity shouldn't be collateral damage.
Built on a geometry of discrete ticks, a radial invariant, and a novel way of segmenting liquidity, Orbital opens the door to risk-aware LP strategies. It allows capital to flow preferentially through the most trustworthy assets, while isolating or "quarantining" tokens that deviate from their peg.
This blog explores the mathematical core of Orbital, contrasts it with Curve and Uniswap v3, and shows why its tick-based segmentation offers a new level of capital efficiency and resilience.
If Curve was the AMM for stablecoins, Orbital might be the AMM for unstable stablecoins.
Curve vs Orbital: Two Philosophies of Stability
At its core, Curve is built on one bold assumption: stablecoins will stay stable. Its invariant, a modification of the constant product, allows low slippage around the 1:1 ratio, but punishes trades harshly as prices drift from the peg. This works beautifully, until it doesn't.
When a stablecoin like USDE depegs, the Curve pool becomes a toxic sinkhole: arbitrageurs drain the valuable assets, leaving LPs with a bag full of risk.
Orbital flips the paradigm.
Instead of assuming pegs hold, Orbital assumes they break. Its design is inherently modular: the pool is split into discrete ticks, each with their own reserves and price boundaries. This segmentation has two profound consequences:
Isolated exposure: If one asset starts to depeg, only the ticks that contain it become affected. Liquidity elsewhere remains protected.
Capital concentration: Liquidity can be deployed selectively toward assets that the LP trusts, say, USDC and USDS, without providing depth to tokens like USDE that carry more risk.
In this sense, Orbital acts like a risk-routing AMM, where liquidity flows dynamically toward the assets with highest trust and tightest pegs.
3. Formalizing Orbital’s Segmented Swap Logic
To understand why Orbital resists depegs, we need to explore its mathematical core, a structure that is both elegant and radically different from other AMMs.
A. The Orbital Invariant
Orbital introduces a novel approach to AMM design by leveraging geometric invariants and radial segmentation of reserve space. Rather than relying on a continuous invariant function like Curve’s StableSwap or a per-tick piecewise structure like Uniswap v3, Orbital discretizes the space into ticks, each associated with a spherical reserve manifold centered at a point:
This construction allows Orbital to organize liquidity radially, relative to the equal-price vector v, and define trades via geometric projections. The operational coordinate used to determine tick order is the normalized projection:
where x^norm = x/r is the reserve vector normalized by the current radius. This scalar coordinate α^norm tells us how far a reserve state is along the direction of the equal-price point, and determines which ticks are interior (active) or boundary (inactive).
When executing a trade, Orbital proceeds as follows:
Segment the trade direction: For an input Δxi, the protocol computes a hypothetical post-trade reserve vector x^pot, and its associated α_int^norm.
Check crossing condition: If the resulting α_int^norm stays between the current interior and boundary tick projections (i.e., satisfies k_bound^max≤α_int^norm≤k_int^min), the trade proceeds within the current tick.
Otherwise, a tick is crossed. The crossover point occurs precisely when:
\(\alpha_{int}^{norm}=k_{cross}^{norm} \Rightarrow \alpha_{cross}=r_{int}\cdot k_{cross}^{norm}\)
To compute the maximum executable trade segment up to this crossover, Orbital solves a constrained optimization under its global invariant. This leads to a nontrivial quadratic equation in the input dimension d_i^cross, derived from:
Plugging this into the invariant equation yields a quadratic (or quartic) that must be solved at each segment:
This procedure may repeat recursively if multiple ticks are crossed during a large trade. Notably, the slippage emerges as the cumulative result of solving the invariant across dynamic geometric boundaries.
B. Depeg Protection and Capital Efficiency
A key innovation in Orbital’s design is its ability to preserve trade functionality even in the presence of a depegged asset. Unlike 2D concentrated liquidity AMMs (like Uniswap v3), where a depeg can paralyze the pool or result in disproportionate exposure, Orbital’s tick-based, topological segmentation ensures that other assets remain tradable at fair value.
This is possible because each tick corresponds to a bounded region in reserve space, and if one asset loses value (say, goes to 0), it only affects the ticks that intersect with that reserve point. The other ticks remain fully functional and capital-efficient.
This not only increases robustness but also unlocks a new form of capital efficiency. Formally, Orbital defines the capital efficiency gain from this bounded exposure as:
where:
x_base is the reserve needed at the equal-price point q
\(x_\text{base} = r\left(1 - \sqrt{\frac{1}{n}}\right),\)x_min is the reserve requirement at the tick boundary defined by the plane constant k
\(x_\text{min}(k),\)and k_depeg is the minimum plane constant needed to support trades when an asset depegs to price p
\(k_\text{depeg}(p).\)
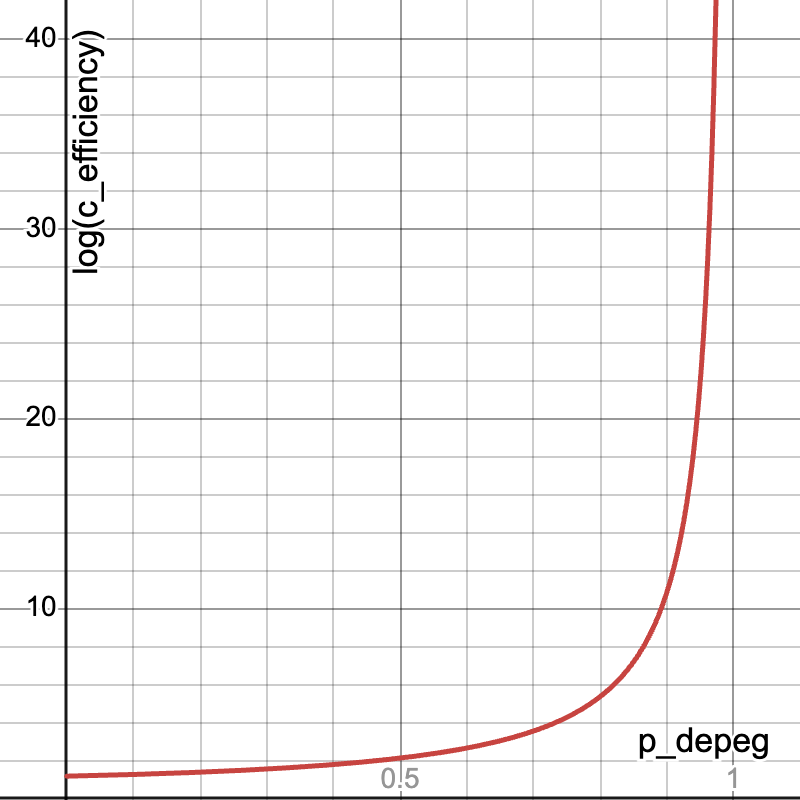
The result is a logarithmic improvement in capital efficiency as the acceptable depeg threshold increases.
Taken from the Paradigm’s Orbital whitepaper, visualizing the exponential gain in capital efficiency as the tick boundary expands to accommodate higher depeg tolerances.
C. Risk Segmentation Emerges Naturally
From this structure, a powerful consequence emerges: LPs can protect themselves from depegs by choosing which ticks to allocate liquidity into.
Liquidity providers can concentrate capital in smaller ticks that are closer to the equal-weight point (e.g. $1 for stables), without having to provision liquidity against catastrophic scenarios. They can explicitly choose a max depeg price p_depeg, and the protocol will compute the optimal tick boundary that covers that risk.
This degree of control and resilience opens the door to risk-aware liquidity provisioning not possible in traditional AMMs.
In contrast, Curve must maintain symmetric exposure across all assets. This is fine if stables are equal. But in practice, they’re not.
4. Practical Implications for LPs and Traders
Orbital's mathematical framework doesn’t just look good on paper, it unlocks concrete strategic advantages for both liquidity providers (LPs) and traders operating in stablecoin markets.
→ For Liquidity Providers
Traditional AMMs force LPs to make binary choices: either provide liquidity across wide price ranges (inefficient) or concentrate capital in a narrow band (risky). In stablecoin pools, this translates to overexposure to a single asset's depeg risk, especially in protocols like Uniswap v3 where the pool's health is compromised if one token collapses in price.
Orbital redefines this tradeoff.
By choosing a tick with a specific depeg tolerance, LPs can target a range of reserve states, effectively saying, “I’m willing to provide liquidity as long as no token depegs below X.” This creates:
Capital-efficient positions with less over-provisioning,
Customizable risk exposure tied to depeg thresholds, and
Tick-based compartmentalization that protects LPs from systemic impact across the entire pool.
This structure is especially valuable in today’s DeFi environment, where the proliferation of new stablecoins (e.g., Ethena’s eUSD, Mountain’s USDM, Sky’s USDS) increases the likelihood of depeg events. LPs no longer need to trust every stablecoin equally, they can design ticks that reflect their subjective confidence in each asset.
→ For Traders
From a trader’s perspective, Orbital provides graceful degradation during volatile events. If one asset collapses, the AMM remains operational, trades between the remaining stablecoins continue at fair prices. This continuity offers:
Reduced slippage in partial depegs,
More reliable price discovery, and
The ability to exit positions even in markets under stress.
Compared to Curve, which offers excellent routing for stables near parity but can suffer from systemic disruptions if one token breaks peg, Orbital enables localized containment of instability. Traders can exploit arbitrage opportunities and move between assets without becoming trapped in dysfunctional pools.
In short: Orbital makes risk-aware DeFi composable. LPs can build concentrated positions without betting on the wrong horse, and traders can interact with stablecoin baskets that degrade gracefully, not catastrophically.
This structural innovation mirrors what Morpho brought to lending, unlocking new strategies by reshaping the underlying topology, but this time, it’s for AMMs.
5. Closing Thoughts: Orbital as the Next Paradigm
Orbital doesn’t just optimize the math behind AMMs it redefines the playing field.
Its topological design unlocks a new layer of expressiveness for both LPs and traders: capital can be deployed based on confidence in peg stability, not just price volatility. The introduction of tick-based compartments and customizable depeg thresholds allows for modular, risk-aware liquidity provision that isn’t possible in Curve or Uniswap v3.
Curve changed the game by tailoring AMMs for stable assets. Morpho did the same for lending, letting users define trust boundaries. Orbital continues that tradition but for stablecoin trading.
As DeFi evolves, protocols will increasingly be judged not only by throughput or slippage, but by how well they degrade under pressure. Orbital’s geometry is not just elegant it’s resilient.
Whether you're building risk-aware vaults, designing stablecoin baskets, or stress-testing your treasury management strategies: Orbital is not just another AMM it’s an engine for modular liquidity logic.
This post builds upon the technical foundations introduced in Paradigm’s Orbital whitepaper. Highly recommended for those interested in the full design.